control-system/Assignment 4 - PI/README.md

# Integral Effect on Control System
This dir is belong to Control System class contains with Integral Effect on Control System. This code 100% original made by my hand :), please leave some notes if you're going to use it. Thanks!

## Software
This program ran in Matlab

## Variables
`s = tf('s');` defines `s` as 'frequency domain' for transfer function and will be used further. 
```
J = 0.01;
b = 0.1;
K = 0.01;
R = 1;
L = 0.5;
```
Those variable comes from BLDC control system.
```
Kp = 1;
% Ki = 1;
% Ki = 3;
% Ki = 5;
Ki = 7;
% Ki = 9;
```
Variable above is the constant from PI control, we're trying to varies the constant to analyze integral effect on control system

## Process
The BLDC motor control system should be defined as transfer function by initialize its numerator-denumerator and *tf()* function.
```
num_motor = [K];
den_motor = [J*L J*R+b*L R*b+K*K];

motor = tf(num_motor,den_motor)
```
Besides the plant function, the PI-control system defined by `C = tf([Kp Ki],[1 0])`. The vector is set according to PI formula which `PI = Kp * Ki/s`. After that, both of system are multiplied each others without feedback by `complete = feedback(motor*C,1);`

That system will be test with step, ramp, and impulse input by call below lines
```
subplot(311), impulse(complete);   % Impulse reponse
subplot(312), step(complete);      % Step Response
subplot(313), step(complete / s);  % Ramp response
stepinfo(complete)
```

Since Matlab doesn't provide any steady-state error calculation, we process it by call below lines
```
[y,t] = step(complete); % Calculate Steady-State error
sse = abs(1 - y(end))
```
Last line works to limit the graph
```
xlim([0 50])
ylim([0 3])
```


## Testing 
For Kp = 1
|   Param	|   Ki = 1	|   Ki = 3	|   Ki = 5	|   Ki = 7	|   Ki = 9	|
|---	|---	|---	|---	|---	|---	|
|   Rise Time	|   22.7723	|   6.7782	|   3.5914	|   2.3175	|   2.3175	|
|   Settling Time	|   40.3716	|   12.1907	|   6.3158	|   3.6779	|  3.6779 	|
|   Overshoot	|   0	|   0	|   0	|   0.3523	|   0	|
|   SSE	|   1.7396e-06	|   0.0034	|   0.0033	|   0.0034	|   6.6536e-05	|

Kp = 1, Ki = 1
![Kp = 1, Ki = 1](https://user-images.githubusercontent.com/77116615/189711219-a3d00c73-0902-4a3f-899c-aca785cf0e6c.png)
Kp = 1, Ki = 3
![Kp = 1, Ki = 3](https://user-images.githubusercontent.com/77116615/189711238-016657a1-8b3d-4209-8033-192464c00bed.png)
Kp = 1, Ki = 5
![Kp = 1, Ki = 5](https://user-images.githubusercontent.com/77116615/189711244-acaa9905-21dc-4e80-915e-c628775a6665.png)
Kp = 1, Ki = 7
![Kp = 1, Ki = 7](https://user-images.githubusercontent.com/77116615/189711248-cdac4205-6511-460d-8eb8-96378564774e.png)
Kp = 1, Ki = 9
![Kp = 1, Ki = 9](https://user-images.githubusercontent.com/77116615/189711253-c2a2208c-fdb8-4640-b419-b2909250ed0e.png)


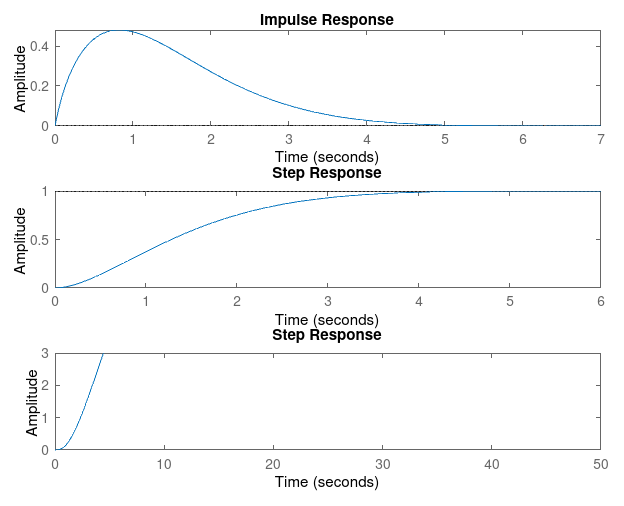
Notes: In theory, SSE should decrease following the increased Ki, but i suspect Matlab just can't compute too much floating point. Hence, i add two additional test below with larger constant to show the effects.

## Additional Testing
For Kp = 50
|   Param	|   Ki = 0	|   Ki = 5	|
|---	|---	|---	|
|   Rise Time	|   0.1201	|   0.1415	|
|   Settling Time	|   0.6376	|   29.5503	|
|   Overshoot	|   19.6150	|   6.1627	|
|   SSE	|    0.1127	|   0.0082	|

Kp = 50, Ki = 0
![Kp = 50, Ki = 0](https://user-images.githubusercontent.com/77116615/189711364-d43497e7-d0f4-4c2d-bdfe-d66c792d7e88.png)
Kp = 50, Ki = 5
![Kp = 50, Ki = 5](https://user-images.githubusercontent.com/77116615/189711372-33a51860-2c9c-4b43-a01c-f31a7f9de2df.png)


## Conclusion
Based on previous tests, we conclude that by adding Integral constant :
* Risie time is **increased**
* Settling time is **increased**
* Overshoot is **decreased**
* SSE is **decreased**

### Notes
Contact nanda.r.d@mail.ugm.ac.id for more information
### Links
You can access the source code here
[github.com/nandard/routh_table.git](https://github.com/nandard/routh_table.git)