3.8 KiB
Integral Effect on Control System
This dir is belong to Control System class contains with Integral Effect on Control System. This code 100% original made by my hand :), please leave some notes if you're going to use it. Thanks!
Software
This program ran in Matlab
Variables
s = tf('s'); defines s as 'frequency domain' for transfer function and will be used further.
J = 0.01;
b = 0.1;
K = 0.01;
R = 1;
L = 0.5;
Those variable comes from BLDC control system.
Kp = 1;
% Ki = 1;
% Ki = 3;
% Ki = 5;
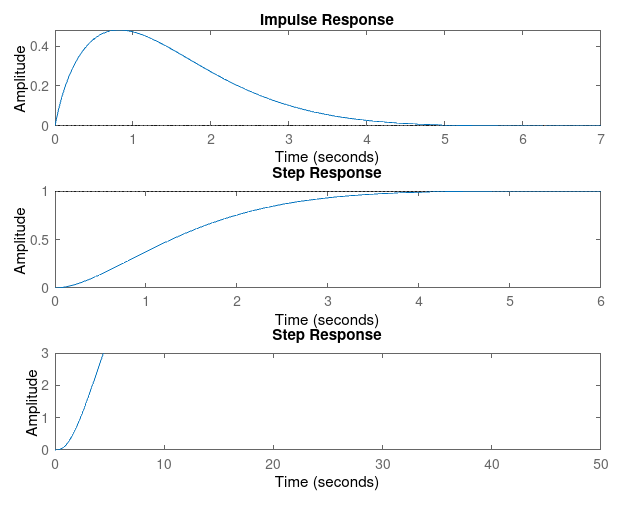
Ki = 7;
% Ki = 9;
Variable above is the constant from PI control, we're trying to varies the constant to analyze integral effect on control system
Process
The BLDC motor control system should be defined as transfer function by initialize its numerator-denumerator and tf() function.
num_motor = [K];
den_motor = [J*L J*R+b*L R*b+K*K];
motor = tf(num_motor,den_motor)
Besides the plant function, the PI-control system defined by C = tf([Kp Ki],[1 0]). The vector is set according to PI formula which PI = Kp * Ki/s. After that, both of system are multiplied each others without feedback by complete = feedback(motor*C,1);
That system will be test with step, ramp, and impulse input by call below lines
subplot(311), impulse(complete); % Impulse reponse
subplot(312), step(complete); % Step Response
subplot(313), step(complete / s); % Ramp response
stepinfo(complete)
Since Matlab doesn't provide any steady-state error calculation, we process it by call below lines
[y,t] = step(complete); % Calculate Steady-State error
sse = abs(1 - y(end))
Last line works to limit the graph
xlim([0 50])
ylim([0 3])
Testing
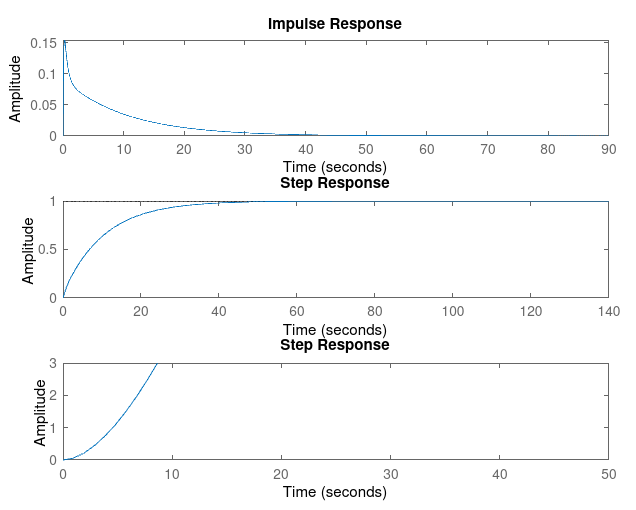
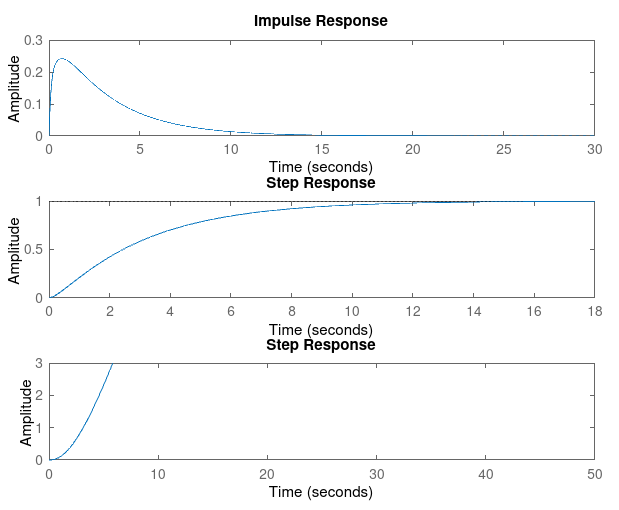
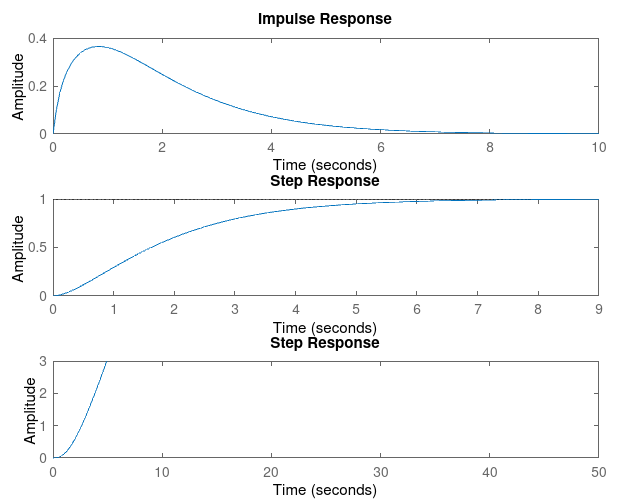
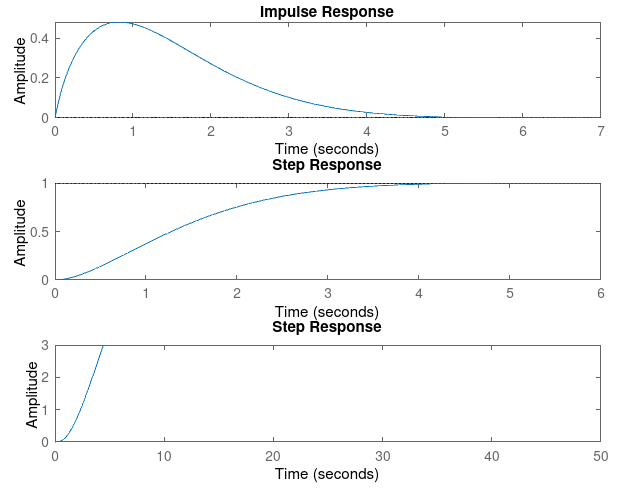
For Kp = 1
| Param | Ki = 1 | Ki = 3 | Ki = 5 | Ki = 7 | Ki = 9 |
|---|---|---|---|---|---|
| Rise Time | 22.7723 | 6.7782 | 3.5914 | 2.3175 | 2.3175 |
| Settling Time | 40.3716 | 12.1907 | 6.3158 | 3.6779 | 3.6779 |
| Overshoot | 0 | 0 | 0 | 0.3523 | 0 |
| SSE | 1.7396e-06 | 0.0034 | 0.0033 | 0.0034 | 6.6536e-05 |
Kp = 1, Ki = 1
Kp = 1, Ki = 3
Kp = 1, Ki = 5
Kp = 1, Ki = 7
Kp = 1, Ki = 9
Notes: In theory, SSE should decrease following the increased Ki, but i suspect Matlab just can't compute too much floating point. Hence, i add two additional test below with larger constant to show the effects.
Additional Testing
For Kp = 50
| Param | Ki = 0 | Ki = 5 |
|---|---|---|
| Rise Time | 0.1201 | 0.1415 |
| Settling Time | 0.6376 | 29.5503 |
| Overshoot | 19.6150 | 6.1627 |
| SSE | 0.1127 | 0.0082 |
Kp = 50, Ki = 0
Kp = 50, Ki = 5
Conclusion
Based on previous tests, we conclude that by adding Integral constant :
- Risie time is increased
- Settling time is increased
- Overshoot is decreased
- SSE is decreased
Notes
Contact nanda.r.d@mail.ugm.ac.id for more information
Links
You can access the source code here github.com/nandard/routh_table.git