Add assignment five

Assignment 5 - PD/README.md

@@ -0,0 +1,93 @@
+# Derivative Effect on Control System
+This dir is belong to Control System class contains with Derivative Effect on Control System. This code 100% original made by my hand :), please leave some notes if you're going to use it. Thanks!
+
+## Software
+This program ran in Matlab
+
+## Variables
+`s = tf('s');` defines `s` as 'frequency domain' for transfer function and will be used further. 
+```
+J = 0.01;
+b = 0.1;
+K = 0.01;
+R = 1;
+L = 0.5;
+```
+Those variable comes from BLDC control system.
+```
+Kp = 1;
+Kd = 1;
+% Kd = 3;
+% Kd = 5;
+% Kd = 7;
+% Kd = 9;
+```
+Variable above is the constant from PD control, we're trying to varies the constant to analyze derivative effect on control system
+
+## Process
+The BLDC motor control system should be defined as transfer function by initialize its numerator-denumerator and *tf()* function.
+```
+num_motor = [K];
+den_motor = [J*L J*R+b*L R*b+K*K];
+
+motor = tf(num_motor,den_motor)
+```
+Besides the plant function, the PD-control system defined by `C = tf([Kd Kp 0],[0 1 0])`. The vector is set according to PD formula which `PD = Kp + Kd * s`. After that, both of system are multiplied each others without feedback by `complete = feedback(motor*C,1);`
+
+That system will be test with step, ramp, and impulse input by call below lines
+```
+subplot(311), impulse(complete);   % Impulse reponse
+subplot(312), step(complete);      % Step Response
+subplot(313), step(complete / s);  % Ramp response
+stepinfo(complete)
+```
+
+Since Matlab doesn't provide any steady-state error calculation, we process it by call below lines
+```
+[y,t] = step(complete); % Calculate Steady-State error
+sse = abs(1 - y(end))
+```
+Last line works to limit the graph
+```
+xlim([0 50])
+ylim([0 3])
+```
+
+
+## Testing 
+For Kp = 1
+|   Param	|   Kd = 1	|   Kd = 3	|   Kd = 5	|   Kd = 7	|   Kd = 9	|
+|---	|---	|---	|---	|---	|---	|
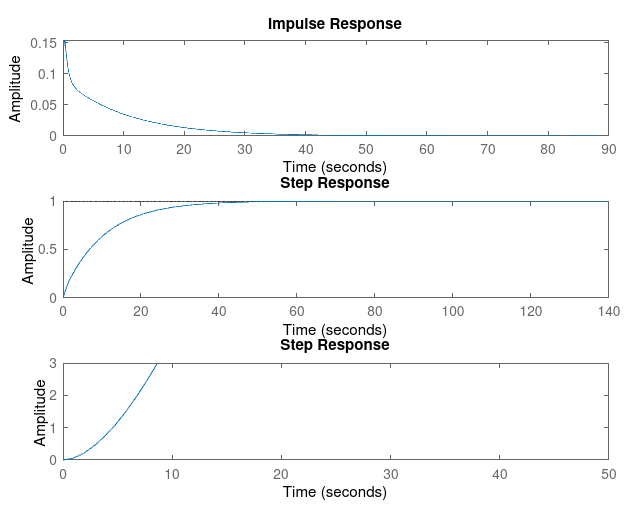
+|   Rise Time	|   0.0540	|   0.0140	|   0.0081	|   0.0057	|   0.0044	|
+|   Settling Time	|   2.1356	|   3.2085	|   3.9313	|   4.6494	|  5.3646 	|
+|   Overshoot	|   50.9930	|   232.5791	|   359.4791	|   452.0385	|   522.2002	|
+|   SSE	|   0.9088	|   0.9077	|   0.9075	|   0.9075	|   0.9069	|
+
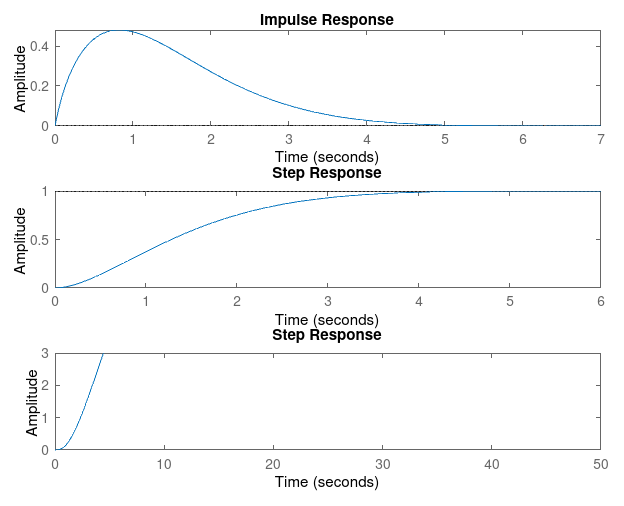
+### Kp = 1, Kd = 1
+
+![Kp = 1, Kd = 1](https://user-images.githubusercontent.com/77116615/189711219-a3d00c73-0902-4a3f-899c-aca785cf0e6c.png)
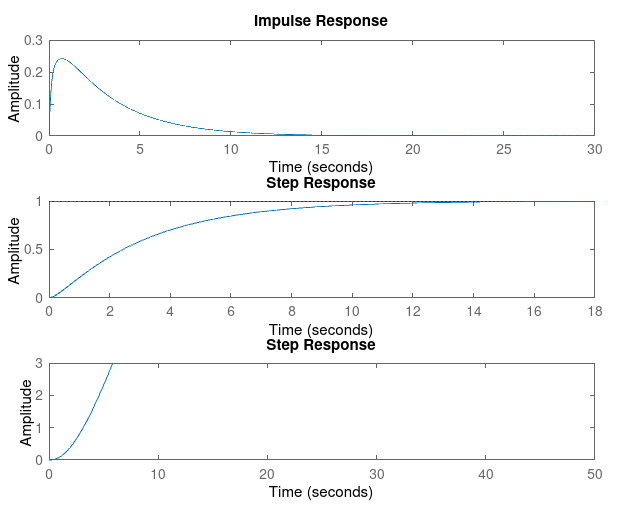
+### Kp = 1, Kd = 3
+
+![Kp = 1, Kd = 3](https://user-images.githubusercontent.com/77116615/189711238-016657a1-8b3d-4209-8033-192464c00bed.png)
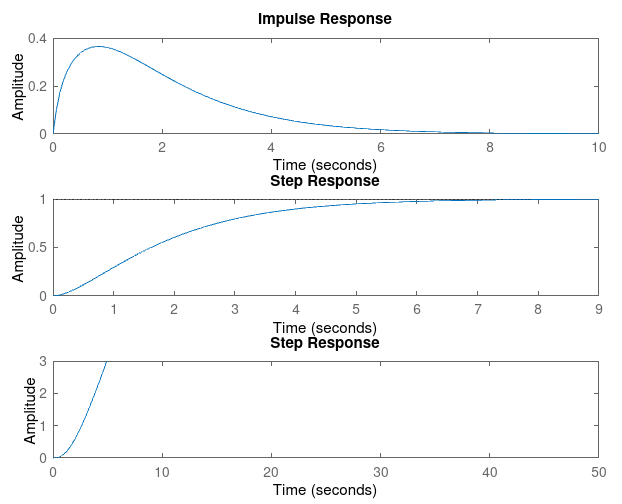
+### Kp = 1, Kd = 5
+
+![Kp = 1, Kd = 5](https://user-images.githubusercontent.com/77116615/189711244-acaa9905-21dc-4e80-915e-c628775a6665.png)
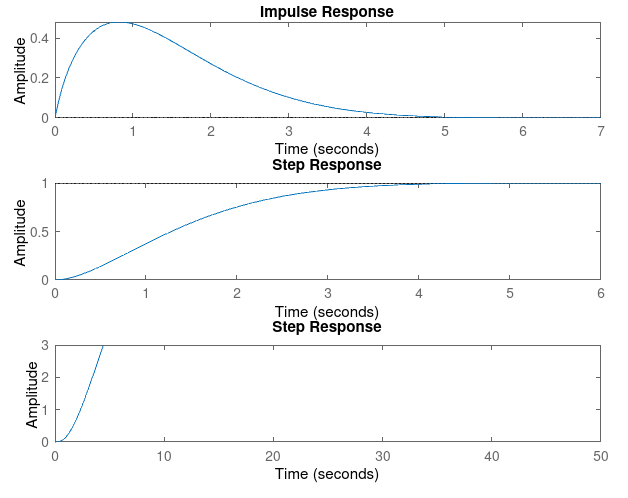
+### Kp = 1, Kd = 7
+
+![Kp = 1, Kd = 7](https://user-images.githubusercontent.com/77116615/189711248-cdac4205-6511-460d-8eb8-96378564774e.png)
+### Kp = 1, Kd = 9
+
+![Kp = 1, Kd = 9](https://user-images.githubusercontent.com/77116615/189711253-c2a2208c-fdb8-4640-b419-b2909250ed0e.png)
+
+## Conclusion
+Based on previous tests, we conclude that by adding Integral constant :
+* Risie time is **increased**
+* Settling time is **increased**
+* Overshoot is **decreased**
+* SSE is **decreased**
+
+### Notes
+Contact nanda.r.d@mail.ugm.ac.id for more information
+### Links
+You can access the source code here
+[github.com/nandard/control-system.git](https://github.com/nandard/control-system.git)

Assignment 5 - PD/week_5.m

@@ -0,0 +1,33 @@
+s = tf('s');
+J = 0.01;
+b = 0.1;
+K = 0.01;
+R = 1;
+L = 0.5;
+
+Kp = 1;
+%Kd = 1;
+%Kd = 3;
+%Kd = 5;
+%Kd = 7;
+Kd = 9;
+    
+num_motor = [K];
+den_motor = [J*L J*R+b*L R*b+K*K];
+motor = tf(num_motor,den_motor)
+
+C = tf([Kd Kp 0],[0 1 0])
+
+complete = feedback(motor*C,1);
+
+subplot(311), impulse(complete);   % Impulse reponse
+subplot(312), step(complete)      % Step Response
+subplot(313), step(complete / s);  % Ramp response
+title("Ramp Response");
+stepinfo(complete)
+
+[y,t] = step(complete); % Calculate Steady-State error
+sse = abs(1 - y(end))
+
+xlim([0 3])
+ylim([0 3])