control-system/Assignment 5 - PD

Derivative Effect on Control System

This dir is belong to Control System class contains with Derivative Effect on Control System. This code 100% original made by my hand :), please leave some notes if you're going to use it. Thanks!

Software

This program ran in Matlab

Variables

s = tf('s'); defines s as 'frequency domain' for transfer function and will be used further.

J = 0.01;
b = 0.1;
K = 0.01;
R = 1;
L = 0.5;

Those variable comes from BLDC control system.

Kp = 1;
Kd = 1;
% Kd = 3;
% Kd = 5;
% Kd = 7;
% Kd = 9;

Variable above is the constant from PD control, we're trying to varies the constant to analyze derivative effect on control system

Process

The BLDC motor control system should be defined as transfer function by initialize its numerator-denumerator and tf() function.

num_motor = [K];
den_motor = [J*L J*R+b*L R*b+K*K];

motor = tf(num_motor,den_motor)

Besides the plant function, the PD-control system defined by C = tf([Kd Kp 0],[0 1 0]). The vector is set according to PD formula which PD = Kp + Kd * s. After that, both of system are multiplied each others without feedback by complete = feedback(motor*C,1);

That system will be test with step, ramp, and impulse input by call below lines

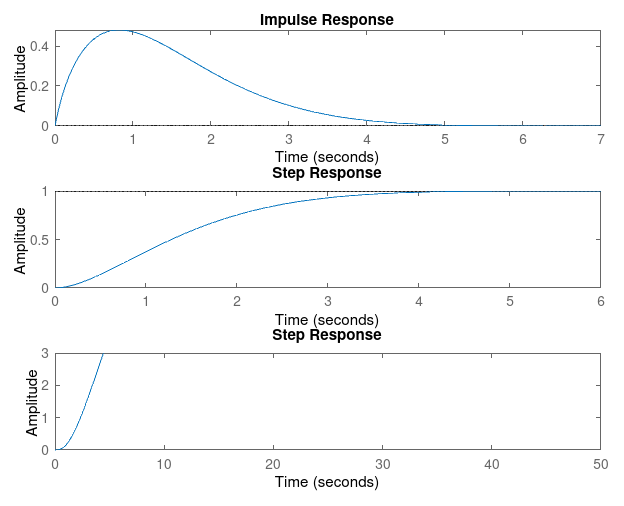
subplot(311), impulse(complete);   % Impulse reponse
subplot(312), step(complete);      % Step Response
subplot(313), step(complete / s);  % Ramp response
stepinfo(complete)

Since Matlab doesn't provide any steady-state error calculation, we process it by call below lines

[y,t] = step(complete); % Calculate Steady-State error
sse = abs(1 - y(end))

Last line works to limit the graph

xlim([0 50])
ylim([0 3])

Testing

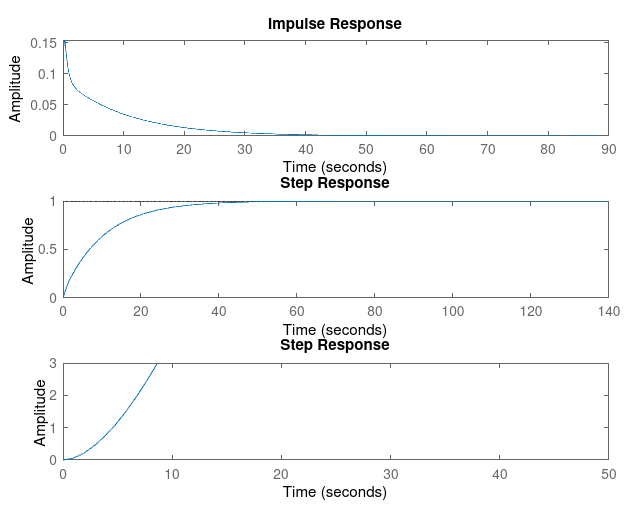
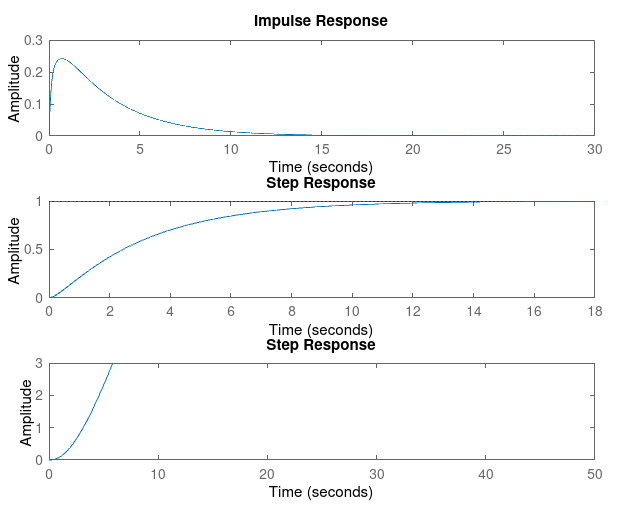
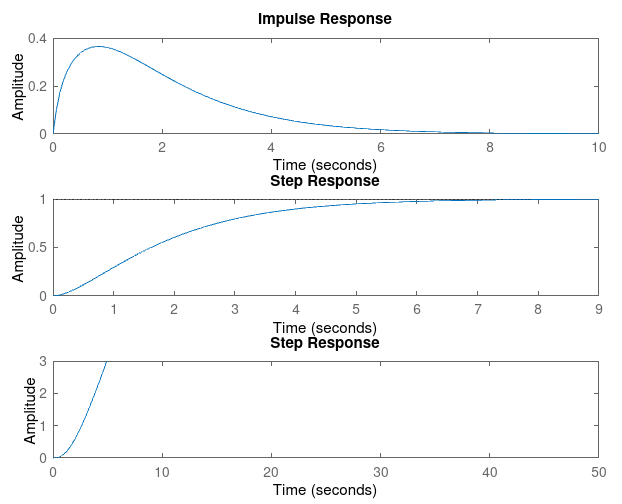
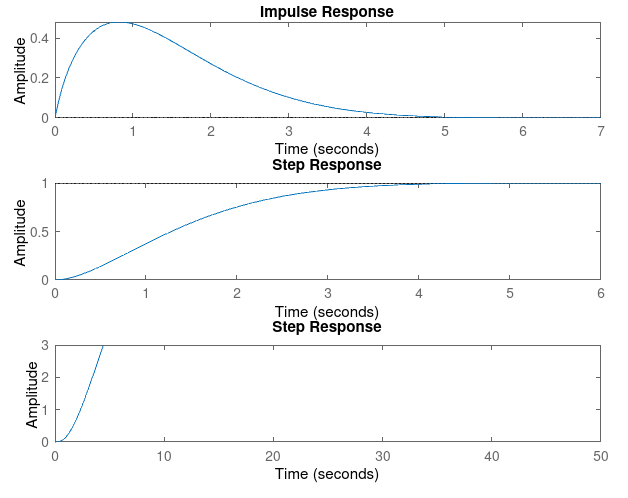
For Kp = 1

Param	Kd = 1	Kd = 3	Kd = 5	Kd = 7	Kd = 9
Rise Time	0.0540	0.0140	0.0081	0.0057	0.0044
Settling Time	2.1356	3.2085	3.9313	4.6494	5.3646
Overshoot	50.9930	232.5791	359.4791	452.0385	522.2002
SSE	0.9088	0.9077	0.9075	0.9075	0.9069

Kp = 1, Kd = 1

Kp = 1, Kd = 3

Kp = 1, Kd = 5

Kp = 1, Kd = 7

Kp = 1, Kd = 9

Conclusion

Based on previous tests, we conclude that by adding Integral constant :

• Risie time is increased
• Settling time is increased
• Overshoot is decreased
• SSE is decreased

Notes

Contact nanda.r.d@mail.ugm.ac.id for more information

Links

You can access the source code here github.com/nandard/control-system.git