mirror of
https://github.com/gabrielkheisa/control-system.git
synced 2026-01-05 02:45:50 +00:00
94 lines
3.1 KiB
Markdown
94 lines
3.1 KiB
Markdown
|
|
# Derivative Effect on Control System
|
||
|
|
This dir is belong to Control System class contains with Derivative Effect on Control System. This code 100% original made by my hand :), please leave some notes if you're going to use it. Thanks!
|
||
|
|
|
||
|
|
## Software
|
||
|
|
This program ran in Matlab
|
||
|
|
|
||
|
|
## Variables
|
||
|
|
`s = tf('s');` defines `s` as 'frequency domain' for transfer function and will be used further.
|
||
|
|
```
|
||
|
|
J = 0.01;
|
||
|
|
b = 0.1;
|
||
|
|
K = 0.01;
|
||
|
|
R = 1;
|
||
|
|
L = 0.5;
|
||
|
|
```
|
||
|
|
Those variable comes from BLDC control system.
|
||
|
|
```
|
||
|
|
Kp = 1;
|
||
|
|
Kd = 1;
|
||
|
|
% Kd = 3;
|
||
|
|
% Kd = 5;
|
||
|
|
% Kd = 7;
|
||
|
|
% Kd = 9;
|
||
|
|
```
|
||
|
|
Variable above is the constant from PD control, we're trying to varies the constant to analyze derivative effect on control system
|
||
|
|
|
||
|
|
## Process
|
||
|
|
The BLDC motor control system should be defined as transfer function by initialize its numerator-denumerator and *tf()* function.
|
||
|
|
```
|
||
|
|
num_motor = [K];
|
||
|
|
den_motor = [J*L J*R+b*L R*b+K*K];
|
||
|
|
|
||
|
|
motor = tf(num_motor,den_motor)
|
||
|
|
```
|
||
|
|
Besides the plant function, the PD-control system defined by `C = tf([Kd Kp 0],[0 1 0])`. The vector is set according to PD formula which `PD = Kp + Kd * s`. After that, both of system are multiplied each others without feedback by `complete = feedback(motor*C,1);`
|
||
|
|
|
||
|
|
That system will be test with step, ramp, and impulse input by call below lines
|
||
|
|
```
|
||
|
|
subplot(311), impulse(complete); % Impulse reponse
|
||
|
|
subplot(312), step(complete); % Step Response
|
||
|
|
subplot(313), step(complete / s); % Ramp response
|
||
|
|
stepinfo(complete)
|
||
|
|
```
|
||
|
|
|
||
|
|
Since Matlab doesn't provide any steady-state error calculation, we process it by call below lines
|
||
|
|
```
|
||
|
|
[y,t] = step(complete); % Calculate Steady-State error
|
||
|
|
sse = abs(1 - y(end))
|
||
|
|
```
|
||
|
|
Last line works to limit the graph
|
||
|
|
```
|
||
|
|
xlim([0 50])
|
||
|
|
ylim([0 3])
|
||
|
|
```
|
||
|
|
|
||
|
|
|
||
|
|
## Testing
|
||
|
|
For Kp = 1
|
||
|
|
| Param | Kd = 1 | Kd = 3 | Kd = 5 | Kd = 7 | Kd = 9 |
|
||
|
|
|--- |--- |--- |--- |--- |--- |
|
||
|
|
| Rise Time | 0.0540 | 0.0140 | 0.0081 | 0.0057 | 0.0044 |
|
||
|
|
| Settling Time | 2.1356 | 3.2085 | 3.9313 | 4.6494 | 5.3646 |
|
||
|
|
| Overshoot | 50.9930 | 232.5791 | 359.4791 | 452.0385 | 522.2002 |
|
||
|
|
| SSE | 0.9088 | 0.9077 | 0.9075 | 0.9075 | 0.9069 |
|
||
|
|
|
||
|
|
### Kp = 1, Kd = 1
|
||
|
|
|
||
|
|
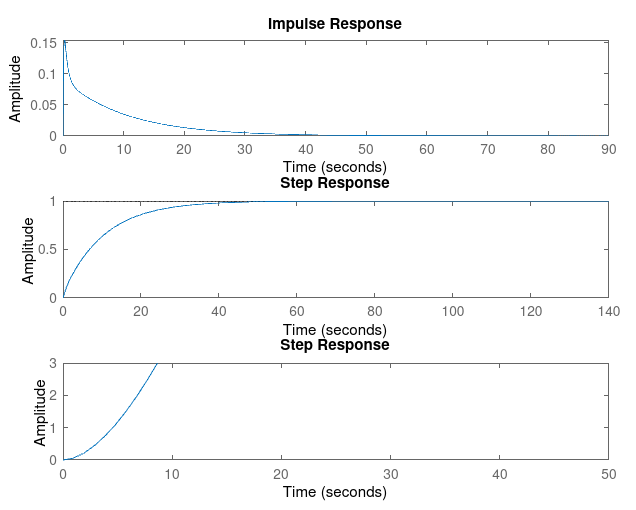
|
||
|
|
### Kp = 1, Kd = 3
|
||
|
|
|
||
|
|
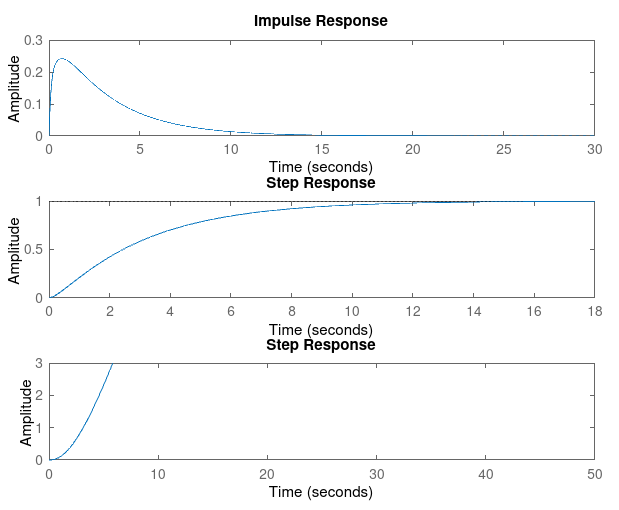
|
||
|
|
### Kp = 1, Kd = 5
|
||
|
|
|
||
|
|
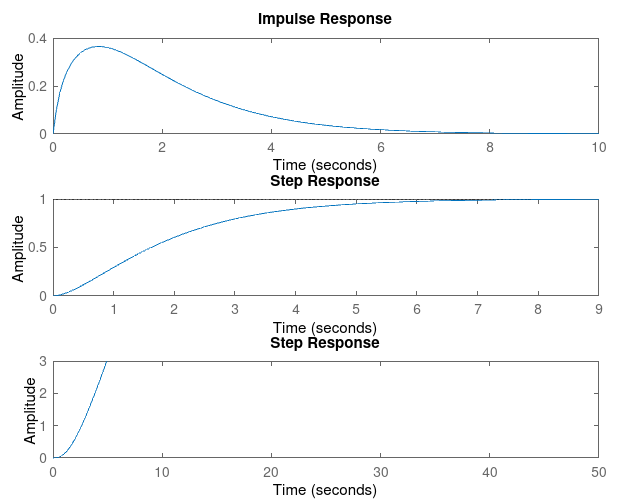
|
||
|
|
### Kp = 1, Kd = 7
|
||
|
|
|
||
|
|
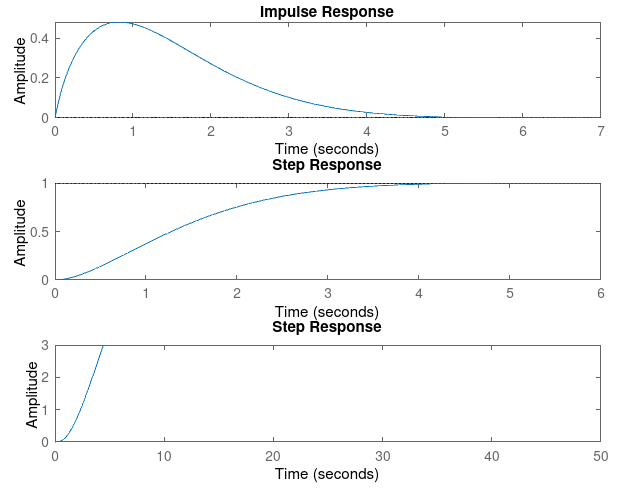
|
||
|
|
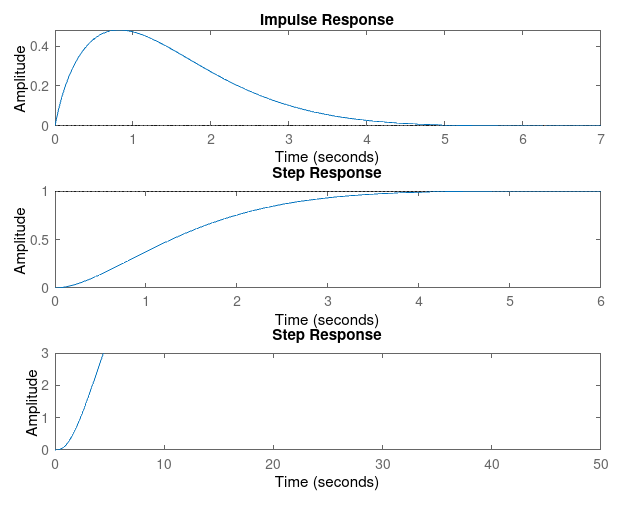
### Kp = 1, Kd = 9
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
## Conclusion
|
||
|
|
Based on previous tests, we conclude that by adding Integral constant :
|
||
|
|
* Risie time is **increased**
|
||
|
|
* Settling time is **increased**
|
||
|
|
* Overshoot is **decreased**
|
||
|
|
* SSE is **decreased**
|
||
|
|
|
||
|
|
### Notes
|
||
|
|
Contact nanda.r.d@mail.ugm.ac.id for more information
|
||
|
|
### Links
|
||
|
|
You can access the source code here
|
||
|
|
[github.com/nandard/control-system.git](https://github.com/nandard/control-system.git)
|